A bolygókerekes hajtóművet széles körben alkalmazzák átviteli mechanizmusként különféle mérnöki gyakorlatokban, például reduktorokban, darukban, bolygókerekes reduktorokban stb. A bolygókerekes reduktor sok esetben helyettesítheti a fix tengelyű fogaskerék-lánc átviteli mechanizmusát. Mivel a fogaskerék-átvitel vonali érintkezés, a hosszú ideig tartó kapcsolódás a fogaskerék meghibásodásához vezet, ezért szükséges a szilárdságának szimulálása. Li Hongli és munkatársai az automatikus kapcsolódási módszert alkalmazták a bolygókerekes hajtómű kapcsolására, és azt kapták, hogy a nyomaték és a maximális feszültség lineáris. Wang Yanjun és munkatársai szintén automatikus generálási módszerrel kapcsolták a bolygókerekes hajtóművet, és szimulálták a bolygókerekes hajtómű statikáját és modális szimulációját. Ebben a cikkben főként tetraéder és hexaéder elemeket használnak a háló felosztására, és a végeredményeket elemzik annak megállapítására, hogy teljesülnek-e a szilárdsági feltételek.

1. Modell létrehozása és eredményelemzés

Bolygókerék háromdimenziós modellezése

Bolygókerékfőként tányérkerékből, napkerékből és bolygókerékből áll. A cikkben kiválasztott fő paraméterek a következők: a belső fogaskerék fogszáma 66, a napkerék fogszáma 36, ​​a bolygókerék fogszáma 15, a belső fogaskerék külső átmérője 150 mm, a modulus 2 mm, a nyomásszög 20°, a fog szélessége 20 mm, az addendum magassági együtthatója 1, a holtjáték-együttható 0,25, és három bolygókerék van.

Bolygókerék statikus szimulációs elemzése

Anyagtulajdonságok meghatározása: importálja az UG szoftverben megrajzolt háromdimenziós bolygókerekes hajtóműrendszert az ANSYS-be, és állítsa be az anyagparamétereket az alábbi 1. táblázat szerint:

Hálózás: A végeselemes háló tetraéderre és hexaéderre van osztva, az elem alapmérete 5 mm. Mivel abolygóműves hajtóműA napkerék és a belső fogaskerék-gyűrű érintkezik és kapcsolódik, az érintkező és a hálós részek hálója tömörített, mérete 2 mm. Először tetraéderes rácsokat használnak, ahogy az az 1. ábrán látható. Összesen 105906 elemet és 177893 csomópontot generálnak. Ezután hexaéderes rácsot alkalmaznak, ahogy a 2. ábrán látható, és összesen 26957 cellát és 140560 csomópontot generálnak.

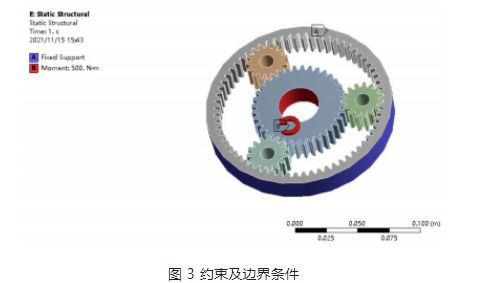
Terhelésalkalmazás és peremfeltételek: a reduktorban lévő bolygókerekes hajtómű működési jellemzői szerint a napkerék a hajtókerék, a bolygókerék a hajtott hajtómű, és a végső kimenet a bolygókerekes tartón keresztül történik. Rögzítse a belső fogaskerék-gyűrűt az ANSYS-ben, és alkalmazzon 500N · m nyomatékot a napkerékre, a 3. ábrán látható módon.

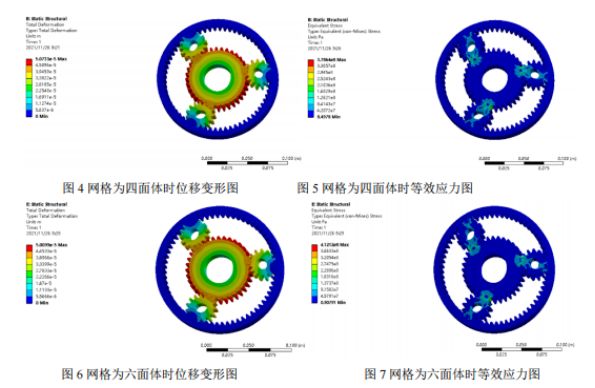
Utófeldolgozás és eredményelemzés: Az alábbiakban a két rácsosztásból származó statikus elemzés során kapott elmozdulás-nefogramot és az azzal egyenértékű feszültség-nefogramot mutatjuk be, és összehasonlító elemzést végeztünk. A kétféle rács elmozdulás-nefogramjából megállapítható, hogy a maximális elmozdulás ott jelentkezik, ahol a napkerék nem kapcsolódik a bolygókerékhez, a maximális feszültség pedig a fogaskerék-kapcsolat tövében jelentkezik. A tetraéderes rács maximális feszültsége 378 MPa, a hatszögletű rács maximális feszültsége pedig 412 MPa. Mivel az anyag folyáshatára 785 MPa, a biztonsági tényező pedig 1,5, a megengedett feszültség 523 MPa. Mindkét eredmény maximális feszültsége kisebb, mint a megengedett feszültség, és mindkettő megfelel a szilárdsági feltételeknek.

2. Következtetés

A bolygómű végeselemes szimulációján keresztül megkapjuk a hajtóműrendszer elmozdulás-deformációs nefogramját és ekvivalens feszültség-nefogramját, amelyekből a maximális és minimális adatok, valamint azok eloszlása ​​abolygóműves hajtóműmodell megtalálható. A maximális egyenértékű feszültség helye egyben az a hely is, ahol a fogaskerék fogai a legnagyobb valószínűséggel meghibásodnak, ezért különös figyelmet kell fordítani rá a tervezés vagy gyártás során. A bolygókerekes hajtómű teljes rendszerének elemzésével kiküszöbölhető az egyetlen fogaskerékfog elemzéséből eredő hiba.