Mire használják az epiciklusos fogaskerekeket?

Epiciklikus fogaskerekekbolygókerekes hajtóműrendszerekként is ismertek, kompakt kialakításuk, nagy hatékonyságuk és sokoldalúságuk miatt széles körben használják különféle iparágakban.

Ezeket a fogaskerekeket elsősorban olyan alkalmazásokban használják, ahol korlátozott a hely, de elengedhetetlen a nagy nyomaték és a sebességváltoztatás.

1. Gépjármű-sebességváltók: Az epiciklikus fogaskerekek kulcsfontosságú alkatrészek az automata sebességváltókban, mivel zökkenőmentes sebességváltást, nagy nyomatékot alacsony fordulatszámon és hatékony erőátvitelt biztosítanak.
2. Ipari gépek: Nehézgépekben használják őket, mivel képesek nagy terheléseket kezelni, egyenletesen elosztani a nyomatékot, és hatékonyan működni kompakt helyeken.
3. Repülőgépipar: Ezek a fogaskerekek kulcsfontosságú szerepet játszanak a repülőgép-hajtóművekben és a helikopterrotorokban, biztosítva a megbízhatóságot és a pontos mozgásvezérlést igénylő körülmények között.
4. Robotika és automatizálás: A robotikában epiciklusos fogaskerekeket használnak a precíz mozgásvezérlés, a kompakt kialakítás és a nagy nyomaték eléréséhez korlátozott helyeken.

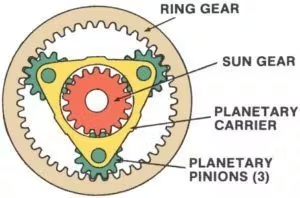
Melyek az epiciklikus fogaskerék-készlet négy eleme?

Egy epiciklikus fogaskerék-készlet, más néven abolygóműves hajtómű rendszer egy rendkívül hatékony és kompakt mechanizmus, amelyet általában autóipari sebességváltókban, robotikában és ipari gépekben használnak. Ez a rendszer négy kulcsfontosságú elemből áll:

1. Sun GearA fogaskerék-készlet közepén elhelyezkedő napkerék a mozgás elsődleges mozgatója vagy vevője. Közvetlenül kapcsolódik a bolygókerekekhez, és gyakran a rendszer bemeneteként vagy kimeneteként szolgál.

2. BolygókerekekEzek több fogaskerékből állnak, amelyek a napkerék körül forognak. Egy bolygókerekes tartóra szerelve kapcsolódnak mind a napkerékhez, mind a tányérkerékhez. A bolygókerekek egyenletesen osztják el a terhelést, így a rendszer képes nagy nyomaték kezelésére.

3.BolygóhordozóEz az alkatrész tartja a bolygókerekeket a helyükön, és támogatja azok forgását a napkerék körül. A bolygóhordozó bemeneti, kimeneti vagy álló elemként működhet a rendszer konfigurációjától függően.

4.Gyűrűs fogaskerék: Ez egy nagy külső fogaskerék, amely körülveszi a bolygókerekeket. A tányérkerék belső fogai kapcsolódnak a bolygókerekekhez. A többi elemhez hasonlóan a tányérkerék is szolgálhat bemenetként, kimenetként, vagy maradhat álló helyzetben.

E négy elem kölcsönhatása rugalmasságot biztosít a különböző sebességarányok és irányváltások eléréséhez egy kompakt szerkezeten belül.

Hogyan lehet kiszámítani az áttételt egy epiciklusos fogaskerék-készletben?

Az áttétel egyepiciklikus fogaskerékkészlet attól függ, hogy mely alkatrészek fixek, bemeneti és kimeneti alkatrészek. Íme egy lépésről lépésre útmutató a sebességváltó áttételének kiszámításához:

1. A rendszerkonfiguráció megértése:

Határozd meg, melyik elem (Nap, bolygóhordozó vagy gyűrű) van álló helyzetben.

Határozza meg a bemeneti és kimeneti komponenseket.

2. Használja az alapvető áttételi egyenletet: Egy epiciklusos hajtóműrendszer áttételi aránya a következőképpen számítható ki:

GR = 1 + (R / S)

Ahol:

GR = Áttétel

R = A fogak száma a tányérkeréken

S = A napkerék fogainak száma

Ez az egyenlet akkor érvényes, amikor a bolygóhordozó a kimenet, és vagy a Nap, vagy a gyűrűfogaskerék álló helyzetben van.

3. Egyéb konfigurációk módosítása:

• Ha a napkerék álló helyzetben van, a rendszer kimeneti sebességét a tányérkerék és a bolygótartó áttétele befolyásolja.
• Ha a tányérkerék álló helyzetben van, a kimeneti sebességet a napkerék és a bolygóhordozó közötti kapcsolat határozza meg.

4. Hátrameneti áttétel kimenet és bemenet között: A sebességcsökkentés kiszámításakor (a bemenet nagyobb, mint a kimenet) az áttétel egyértelmű. A sebesség szorzásához (a kimenet nagyobb, mint a bemenet) invertáljuk a kiszámított áttételt.

Példa számítás:

Tegyük fel, hogy egy fogaskerék-készlet a következő tulajdonságokkal rendelkezik:

Tányérkerék (R): 72 fog

Napkerék (S): 24 fogú

Ha a bolygóhordozó a kimenet és a napkerék álló helyzetben van, akkor az áttétel:

GR = 1 + (72/24) GR = 1 + 3 = 4

Ez azt jelenti, hogy a kimeneti sebesség négyszer lassabb lesz, mint a bemeneti sebesség, ami 4:1-es csökkentési arányt biztosít.

Ezen alapelvek megértése lehetővé teszi a mérnökök számára, hogy hatékony és sokoldalú rendszereket tervezzenek, amelyek az adott alkalmazásokhoz igazodnak.